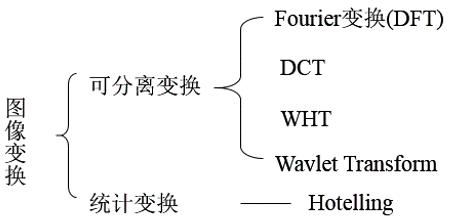
图像变换

图像变换

• 图像变换
• 3.1 图像变换的预备知识
  • 图像变换的基本概念（目的、要求、基本方法）
• 3.2 傅里叶变换及其性质
• 卷积定理与相关定理
• 图书文献

3.1 图像变换的预备知识

图像变换的基本概念（目的、要求、基本方法）

1. 图像变换的目的

• 使图像处理问题简化

• 有利于图像特征提取
• 有助于从概念上(物理上)增强上对图像信息的理解

2. 图像变换的要求

• 图像变换通常是一种__二维正交变换__,一般要求:

  1. 正交变换必须是__可逆__的

     • 因为通常我们需要将在变换域对图像进行处理后，再将其变换到空间域进行表达显示

  2. 正变换和反变换的算法不能太复杂;

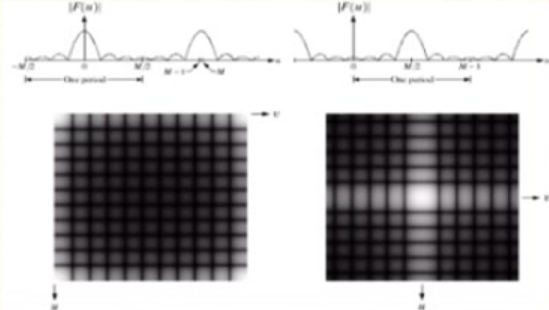
  3. 正交变换的特点（能量保持，重新分配，能量集中）

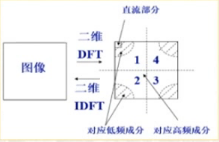
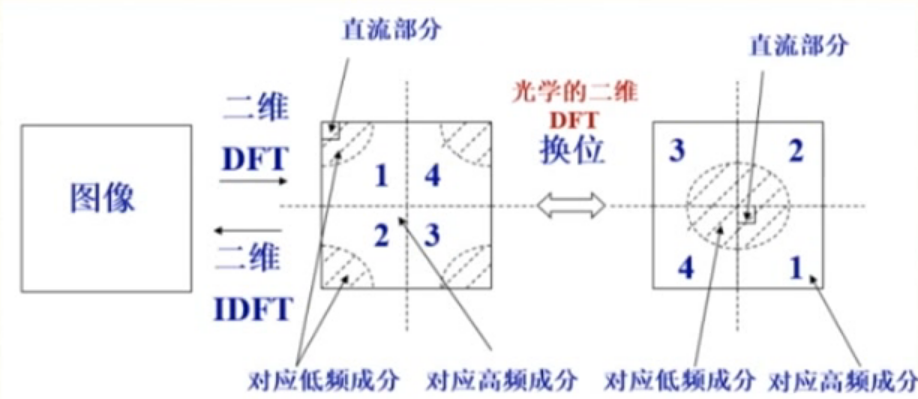
     • 在变换域中图像能量将__集中分布在低频率成分上__,
     • 边缘、线状信息反应在高频率成分上
     • 这将有利于图像处理

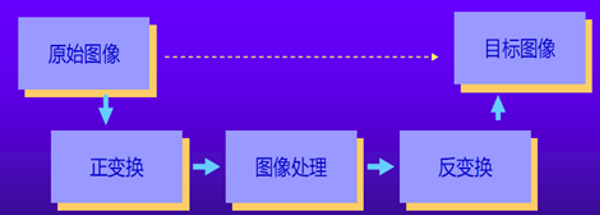
3. 图像变换的基本方法

• 时域信号变换到频域，处理，后再回到时域。
• 
• 

二维离散傅里叶变换DFT

• 傅立叶变换的定义(见$二维傅立叶变换.md$)

• 傅立叶变换可以看作数学上的棱镜,可以__将函数基于频率分解为不同的成分__.

• 离散二维傅里叶变换

  • 

3.2 傅里叶变换及其性质

• 可分离性

  • 二维离散傅立叶变换DFT可分离性的基本思想是二维DFT可以分离为两次(轮)一维DFT;

  • 一个$M*N$的二维图像$f(x,y)$

    • 先按行对列变量$y$做一次长度为$N$的一维离散傅立叶变换
    • 再将结果按列向量对$x$做一次长度为M的傅立叶变换就可以得到图像的傅立叶变换
    • $F(u,v)=\frac{1}{MN}\sum_{x=0}^{M-1}{\left[\sum_{y=0}^{N-1}f(x,y)e^{\frac{-j2\pi vy}{N}}\right]}e^{\frac{-j2\pi ux}{M}}\\ F(x,v)=\frac{1}{N}\sum_{y=0}^{N-1}{f(x,y)e^{\frac{-j2\pi vy}{N}}},v=0,1,...,N-1\\ F(u,v)=\frac{1}{M}\sum_{x=0}^{M-1}{F(x,v)e^{\frac{-j2\pi ux}{M}}},u=0,1,...,M-1$

  • 

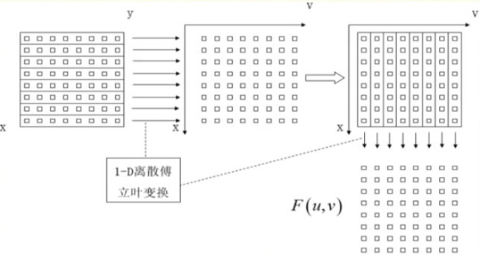
  • 同理,2d逆变换也可以类似进行.

• 周期性和共轭对称性

  • 由傅立叶变换的基本性质可以知道,离散信号的频谱具有周期性,其正变换和逆变换都是以点数$N$为周期的;

    • 一维DFT:$F(u)=F(u\pm kN),k\in \mathbb{Z}$
    • 二维DFT:$F(u,v)=F(u\pm kM,v\pm iN),k,i\in \mathbb{Z}$

  • 傅立叶变换的结果是以原点为中心的共轭对称函数

    • 一维$F(u)=F^{*}(-u)$
    • 二维$F(u,v)=F^{*}(-u,-v)$
    • 

• 平移性质

  • 若$f(x)\Leftrightarrow F(u)$，则有$f(x)e^{\frac{j2\pi xu_0}{N}} \Leftrightarrow F(u-u_0)$

  • 若$f(x,y)\Leftrightarrow F(u,v)$，则由$f(x,y)e^{j2\pi\left( x\frac{u_0}{M} + y\frac{v_0}{N} \right) } \Leftrightarrow F(u-u_0,v-v_0)$

• 在数字图像处理中，需要频谱中心化(将$F(u,v)$的原点移动到$M*N$频域的中点),所以一般需要乘以一个因子,即令上式的$u_0=\frac{M}{2},v_0=\frac{N}{2}$.

  • 当空间域$f(x,y)$产生移动时,在频域只发生相位移动,并不影响幅度值.
  • 

• 旋转性质

  • 若$f(x,y)$旋转了一个角度,那么$f(x,y)$旋转后的图像的傅立叶变换也会旋转相同的角度.
  • 在极坐标系中
  • $\begin{cases}x=r\cos{\theta}\\ y=r\sin{\theta}\\ \end{cases} \begin{cases} u=\omega \cos{\phi}\\ v=\omega \sin{\phi}\\ \end{cases}\\ f(x,y)\to f(r,\theta) \Leftrightarrow F(\omega , \phi )$

若$f(x,y)$被选择$\theta_0$,则$F(u,v)$也会被旋转同一角度,即有

$f(r,\theta + \theta_0) \Leftrightarrow F(\omega, \phi + \theta_0 )$

原图像及其傅里叶变换	原图像旋转45° 及其傅里叶变换

​

• 证明过程1

  $f(x,y)$旋转$\theta_0$后得到$g(x',y')$,利用旋转公式可以得到

$\left( \begin{matrix} x'\\ y' \end{matrix} \right)= \left( \begin{matrix} \cos{\theta_0} &\sin{\theta_0} \\ -\sin{\theta_0} &\cos{\theta_0} \end{matrix} \right) \left( \begin{matrix} x\\ y \end{matrix} \right)$

​ 则:

$\left( \begin{matrix} x\\ y \end{matrix} \right)= \left( \begin{matrix} \cos{\theta_0} &-\sin{\theta_0} \\ \sin{\theta_0} &\cos{\theta_0} \end{matrix} \right) \left( \begin{matrix} x'\\ y' \end{matrix} \right)$

• 则$g(x',y')$的连续二维傅里叶变换为:

$x = \cos{\theta_0}x'-\sin{\theta_0}y'\\ y = \sin{\theta_0}x'+\cos{\theta_0}y'$

所以

$\begin{aligned} &\int_{-\infty}^{+\infty}{\int_{-\infty}^{+\infty}{g(x',y')e^{-j2\pi (ux+vy)}}dxdy} \\ =&\int_{-\infty}^{+\infty}{\int_{-\infty}^{+\infty}{g(x',y')e^{-j2\pi (u(\cos{\theta_0}x'-\sin{\theta_0}y')+v(\sin{\theta_0}x'+\cos{\theta_0}y'))}}d(\cos{\theta_0}x'-\sin{\theta_0}y')d(\sin{\theta_0}x'+\cos{\theta_0}y')}\\ \end{aligned}$

又因为(忽略高阶无穷小)

$\begin{aligned} & d(\cos{\theta_0}x'-\sin{\theta_0}y')d(\sin{\theta_0}x'+\cos{\theta_0}y') \\ =& \left( \cos{\theta_0}dx' - \sin{\theta_0}dy' \right)\left( \sin{\theta_0}dx' + \cos{\theta_0}dy'\right)\\ \approx& (\cos{\theta_0} + \sin{\theta_0})dx'(\cos{\theta_0} - \sin{\theta_0})dy' \end{aligned}$

且

$\begin{aligned} & & u(\cos{\theta_0}x'-\sin{\theta_0}y')+v(\sin{\theta_0}x'+\cos{\theta_0}y')\\ &=& x'(u\cos{\theta_0} + v\sin{\theta_0}) + y'(v\cos{\theta_0}-u\sin{\theta_0})\\ \end{aligned}$

所以:

$\begin{aligned} &\int_{-\infty}^{+\infty}{\int_{-\infty}^{+\infty}{g(x',y')e^{-j2\pi ( x'(u\cos{\theta_0} + v\sin{\theta_0}) + y'(v\cos{\theta_0}-u\sin{\theta_0}))}}(\cos{\theta_0} + \sin{\theta_0})dx'(\cos{\theta_0} - \sin{\theta_0})dy' }\\ =& G(u\cos{\theta_0+v\sin{\theta_0},-u\sin{\theta_0}+v\cos{\theta_0}}) \end{aligned}$

也即$F(u,v)$旋转后的图像.

• 证明过程2:

  

卷积定理与相关定理

卷积定理

• 空间域卷积

  • 两个空间域信号的卷积等价于其频率域信号的乘积
  $f(x,y)*h(x,y) \Leftrightarrow F(u,v)H(u,v)$

• 频率域卷积

  • 两个频率域信号的卷积等价于其空间与信号的乘积
  $f(x,y)h(x,y) \Leftrightarrow F(u,v)*H(u,v)$

• 卷积定理可以将复杂的卷积运算化为简单的乘法运算,方便滤波操作.

相关定理

• 空间域的$f(x,y)$与$g(x,y)$的相关操作等价于频率域的$F(u,v)$的共轭与$G(u,v)$相乘

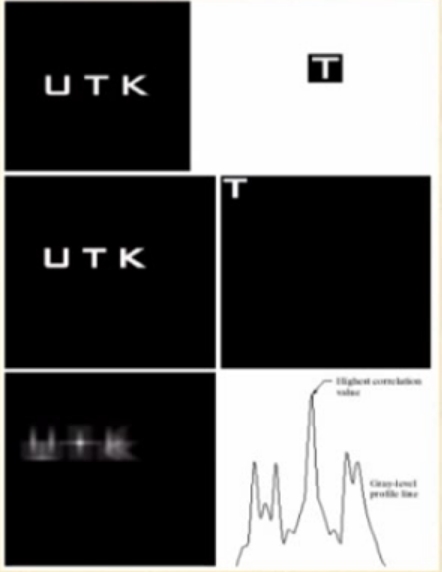
$f(x,y)\circ g(x,y) \Leftrightarrow F^*(u,v)G(u,v)\\ f^*(x,y)\circ g(x,y) \Leftrightarrow F(u,v)G(u,v)$

• 应用于匹配场合
  • 相关的重要应用在于匹配，确定是否有感兴趣的物体区域。$f(x,y)$是原始图像，$g(x,y)$作为感兴趣的物体或区域（模板），如果匹配，两个函数的相关值会在f中找到相应g点的位置上达到最大值。如图所示。图像$f(x,y)$与模板$g(x,y)$，通过计算相关函数，在匹配点处达到最大值，如图中红色圆圈标注的区域。 +

相关系数与相关函数(补充)

• 在一维情况下:

  • 相关系数:表征两个信号$f_1(t)$与$f_2(t)$的相似程度;

  • 若$C_{12}f_2(t)$来逼近$f_1(t)$,设$f_1(t)$和$f_2(t)$均为__能量有限信号__.

    • 定义能量误差
    $\overline{\epsilon^2}=\int_{-\infty}^{+\infty}\left[ f_1(t) -C_{12}f_2(t)\right]^2dt$
    • 要求$\overline{\epsilon^2}$的最小值,就得找到$\overline{\epsilon^2}(C_{12})$的极点,令
  $\begin{aligned} \frac{d\overline{\epsilon^2}}{dC_{12}}&=0\\ C_{12}&=\frac{\int_{-\infty}^{+\infty}f_1(t)f_2(t)dt}{\int_{-\infty}^{+\infty}f_2^2(t)dt} \end{aligned}$
  • 则__相对能量误差__:
  $\begin{aligned} \frac{\overline{\epsilon^2}}{\int_{-\infty}^{+\infty}f_1^2(t)dt} =&1 - \frac{\left[\int_{-\infty}^{+\infty}f_1(t)f_2(t)dt\right]^2}{\int_{-\infty}^{+\infty}f_1^2(t)dt\int_{-\infty}^{+\infty}f_2^2(t)dt}\\[2ex] =&1-\rho_{12}^{2} \end{aligned}$

  • 定义相关系数$\rho_{12}$

    • $\rho_{12}=\frac{\int_{-\infty}^{+\infty}f_1(t)f_2(t)dt}{\sqrt{\int_{-\infty}^{+\infty}f_1^2(t)dt}\sqrt{\int_{-\infty}^{+\infty}f_2^2(t)dt}}$
    • $\rho_{12} = \frac{\left<f_1(t),f_2(t)\right>}{||f_1(t)||_2||f_2(t)||_2}$
    • $-1\le \rho_{12} \le 1$
    • $\rho = 0$ 表示两信号正交.

  • 相关系数:

    • 无时差时相关系数
    $\rho_{12} = \frac{\left<f_1(t),f_2(t)\right>}{||f_1(t)||_2||f_2(t)||_2}=\frac{R_{12}(0)}{||f_1(t)||_2||f_2(t)||_2}$
    • 有时差时相关系数
    $\rho_{12} = \frac{\left<f_1(t),f_2(t)\right>}{||f_1(t)||_2||f_2(t)||_2}=\frac{R_{12}(\tau)}{||f_1(t)||_2||f_2(t)||_2}$
    • 定义__互相关函数__:
    $\begin{aligned} R_{12}(\tau) &=& \int_{-\infty}^{+\infty}f_1(t)f_2(t-\tau)dt = \int_{-\infty}^{+\infty}f_1(t+\tau)f_2(t)dt\\ R_{21}(\tau) &=& \int_{-\infty}^{+\infty}f_1(t-\tau)f_2(t)dt = \int_{-\infty}^{+\infty}f_1(t)f_2(t+\tau)dt\\ \end{aligned}$
    • 互相关函数的性质
    $R_{12}(\tau)\ne R_{21}(\tau),R_{12}(\tau) = R_{21}(-\tau)$
    • 若$f_1(t)=f_2(t)=f(t)$,则定义__自相关函数__:
    $R(\tau) = \int_{-\infty}^{+\infty}f(t)f(t-\tau)dt=\int_{-\infty}^{+\infty}f(t+\tau)f(t)dt$

    性质:

    $R(\tau) = R(-\tau)$

图书文献

MOOC《数字图像处理》——武汉大学——3. 图像变换