像增强-空间域增强
# 图像增强技术
# 5 空间域增强——图像平滑
图像平滑也称为图像去噪,是为了抑制图像噪声改善图像质量进行的处理。
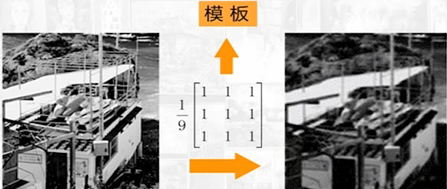
几种空间域的图像平滑方法:
- 邻域平均法
- 超限像素平滑法
- 由选择包边缘平滑法
- 中值滤波法
# 邻域平均法
直接在空间域上进行平滑处理。
思想:假设图像由灰度恒定的小块组成,相邻的像素之间存在很高的相关性,而噪声则是统计独立的。所以可以用邻域内各像素的灰度平均值代替原来的灰度值,实现图像的平滑。
原图像为N×N大小的f(i,j),平滑后的图像为g(x,y),则
g(x,y)=M1i,j∈s∑f(i,j)其中s为邻域矩阵,M为邻域矩阵的像素个数。
若为3×3的邻域平均法,对像素 (m,n),其领域像素如图中黄色所示
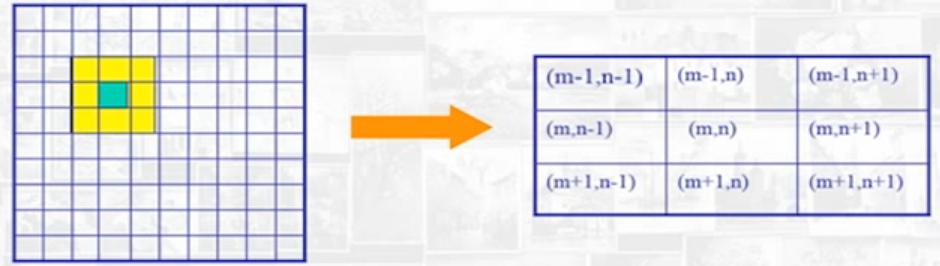
- 则相当于用矩阵A与图像f(m,n)进行卷积,其中
Ag(m,n)=91⎣⎢⎡111111111⎦⎥⎤=91i∈Z∑j∈Z∑f(m+i,n+j)我们假设图像中的噪声是随机不相关的加性噪声,窗口内各点的噪声是独立同分布的,经过平滑后,信号与噪声的方差比可望提高M倍。
优点:算法简单。
缺点:在降低噪声的同时会使得图像产生模糊,特别是在边缘和细节处,而且邻域越大,去噪能力增强的同时模糊程度越严重。

为了客服简单局部平均法的缺点,目前提出了许多保边缘、细节的局部平滑算法,如超限像素平滑法。
# 超限像素平滑法
对邻域平均法稍加改进,把f(x,y)和邻域平均得到的g(x,y)值做一个差的绝对值,再与选定的阈值做比较,用比较的结果决定(x,y)位置的灰度值g′(x,y):
g′(x,y)=⎩⎪⎨⎪⎧g(x,y),∣f(x,y)−g(x,y)∣≥Tf(x,y),∣f(x,y)−g(x,y)∣≤T特点:
- 能有效抑制椒盐噪声
- 能较好的保护微小灰度差的细节和纹理。

同局部平滑法相比,超限像元平滑法去椒盐噪声的效果更好。而且可以保护有微小灰度差的细节和纹理。
# 有选择保边缘平滑法
- 对图像上任一像素x,y的5×5邻域,采用9个掩模,包括3×3,4个五边形,4个六边形。
- 计算对应各个掩模覆盖的9种组合各自所包含数据的均值和方差,对方差进行排序,最小方差所对应的掩模区的灰度均值就是像素(x,y)的输出值。
- 这种方法用方差 来测度区域的灰度均匀性
- 如果区域含有尖锐的边缘,灰度方差就会很大
- 如果区域不含边缘或灰度均匀,方差就小
- 故最小方差所对应的区域就是灰度最均匀的区域
- 这种平滑方法既能消除噪声,由不会破坏区域边界的细节。
- 五边形和六边形在(x,y)处都有锐角,即便像素(x,y)位于一个复杂形状区域的锐角处,也能找到均匀的区域。从而在平滑时既不会使得尖锐边缘模糊,也不会破坏边缘形状。
# 中值滤波法
- 用一个滑动窗口,对窗口内的像素灰度值排序,用中值代替窗口中心像素的灰度值,是一种非线性的图像平滑法。
- 中值滤波法对脉冲干扰及椒盐噪声的抑制效果很好,在抑制随机噪声的同时,还能够保护边缘少受模糊。
- 但对点、线细节较多的图像不太适合。
- 最重要的环节:选择窗口尺寸的大小
- 通常很难事先就确定出最佳的窗口尺寸,需要通过从小窗口到大窗口的中值滤波试验,再从中选取最合适的窗口。
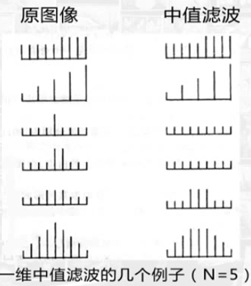
- 离散阶跃信号、斜升信号没有受到影响。
- 离散三角信号的顶部则变平了。对于离散的脉冲信号,当连续出现的次数小于窗口尺寸的一半时,将被抑制掉。否则将不受影响。
二维中值滤波器的窗口形状可以有很多种,如线状,方形,十字行形,圆形,菱形等。
- 方形或圆形适宜于外轮廓线较长的物体图像;
- 十字形窗口对有尖顶角状的图像效果好。


# 6 空间域增强——图像锐化
- 锐化的目的是增强图像的边缘或轮廓。
- 图像的平滑是通过积分过程使图像边缘模糊,而图像锐化是通过微分过程使图像边缘突出、清晰。
- 锐化提高图像的高频分量,增加灰度反差增强图像的边缘和轮廓,以便后期图像识别。
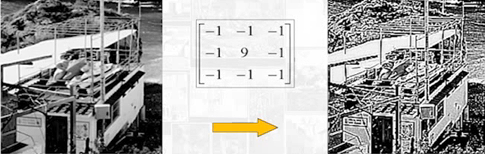
最常使用的图像锐化法-梯度法
# 1. 一阶导数法--梯度法
对于左图,左侧的边是正的(由暗到亮),右侧的边是负的(由亮到暗)。对于右图,结论相反。常数部分为零。
# 梯度算子 Gradient operators
- 图像f(x,y)在(x,y)处的梯度为
- 梯度是一个具有大小和方向的矢量。
- 梯度的方向就是函数f(x,y)在(x,y)处最大变化率的方向。
# 梯度算子(水平垂直的差分法)
对于离散图像出来说,经常用梯度的大小,来表示“梯度”,所以上式的一阶偏导可以用一阶差分来近似表示,即
fx′=f(x+1,y)−f(x,y)fy′=f(x,y+1)−f(x,y)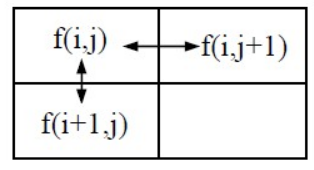
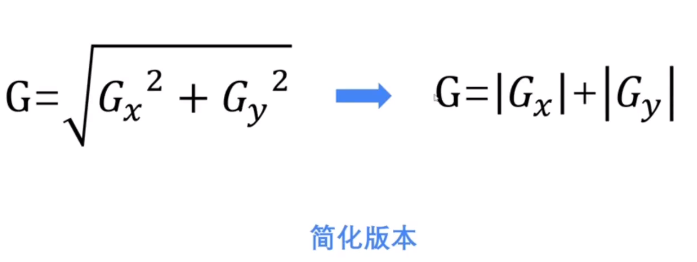
为了简化梯度的计算,通常使用
grad(x,y)=max(∣fx′∣,∣fy′∣)grad(x,y)=∣fx′∣+∣fy′∣对应的梯度算子(滤波模板形式)为:
[−1,1]or[−1,1]T
除了梯度算子以外,还有Roberts,Prewitt和Soble算子也可以用来计算梯度,增强边缘。
# Roberts算子(对角相差的差分法)
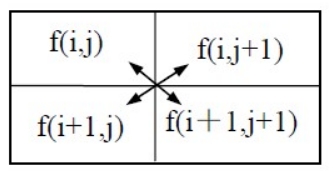
差分计算式为fx′=∣f(x+1,y+1)−f(x,y)∣,fy′=∣f(x+1,y)−f(x,y+1)∣
对应的算子为
其中左侧对接近45°的边缘有较强响应,右侧对接近-45°的边缘有较强响应。
imgPath = 'E:\opencv_pic\src_pic\pic6.bmp';
img = imread(imgPath);
img=rgb2gray(img);
w1 =[-1,0; 0,1];
w2 =[0,-1; 1, 0];
G1=imfilter(img, w1, 'corr', 'replicate');
G2=imfilter(img, w2, 'corr', 'replicate');
G=abs(G1)+abs(G2);
subplot(2,2,1),imshow(img), title('原始图像');
subplot(2,2,2),imshow(abs(G1)), title('w1图像');
subplot(2,2,3),imshow(abs(G2)),title('w2滤波');
subplot(2,2,4),imshow(G),title('Robert交叉梯度图像');
2
3
4
5
6
7
8
9
10
11
12
13
# Prewitt算子
加大了边缘增强算子的模板大小,由2×2扩大到3×3
目的:在边缘锐化的同时减少噪声的影响。而梯度算子和Roberts算子均不能避免噪声影响
Prewitt算子的矩阵形式是:
⎣⎢⎡−1−1−1000111⎦⎥⎤and⎣⎢⎡−101−101−101⎦⎥⎤
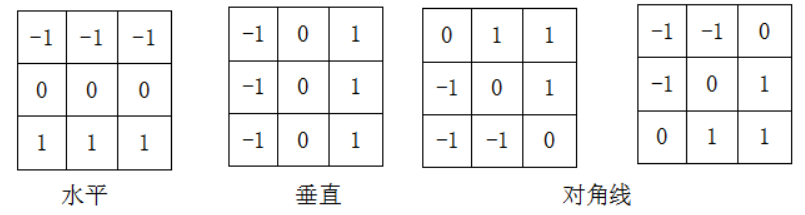
# Sobel算子(对4领域采用带权方法计算)
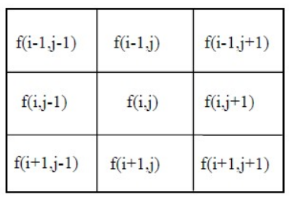
Sobel算子是在Prewitt算子的基础上改进的,在中心系数上使用一个权值2,相比较Prewitt算子,Sobel模板能够较好的抑制(平滑)噪声。但检测边缘较宽
Sobel算子的矩阵形式是(对4邻域的权重加大了):
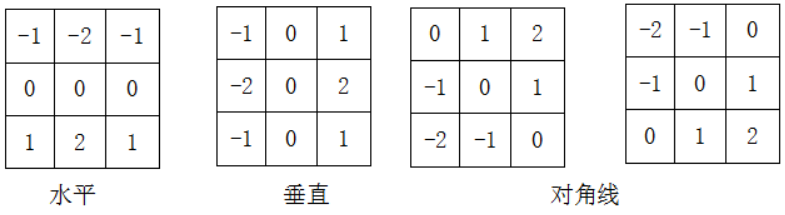
| 计算公式(垂直) | 计算公式(水平) |
|---|---|
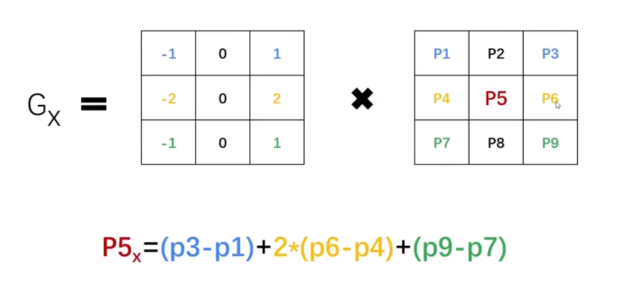 | 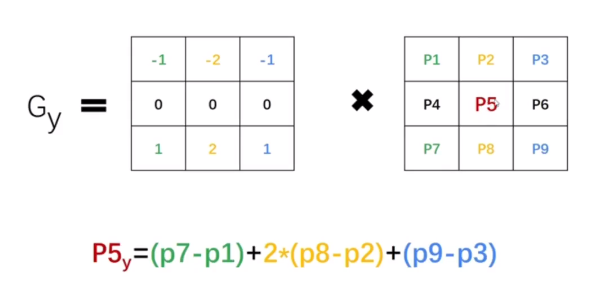 |
# 计算近似梯度值

imgPath = 'E:\opencv_pic\src_pic\pic6.bmp';
img = imread(imgPath);
img=rgb2gray(img);
w1 =[-1,-2,-1; 0,0,0; 1,2, 1];
w2 =[ -1,0,1; -2,0,2; -1,0,1];
G1=imfilter(img, w1);
G2=imfilter(img, w2);
G=abs(G1)+abs(G2);
subplot(2,2,1),imshow(img), title('原始图像');
subplot(2,2,2),imshow(abs(G1)), title('w1图像');
subplot(2,2,3),imshow(abs(G2)),title('w2滤波');
subplot(2,2,4),imshow(G),title('Sobel交叉梯度图像');
2
3
4
5
6
7
8
9
10
11
12
13
14
# scharr算子
- scharr算子的矩阵形式是(对4邻域的权重加大了)
- scharr算子比sobel算子的精确度更高
- 从卷积核可以看到,他的精确度体现在系数上的差别
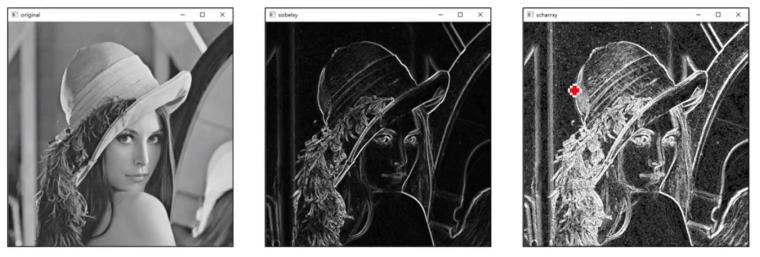
- 右侧的scharry算子的精度更高
# 梯度阈值控制
第一种输出形式:根据梯度计算式,直接采用梯度算子输出g(x,y)=grad(x,y),仅显示灰度变化比较陡的边缘轮廓,而灰度变化比较平缓或均匀的区域则呈黑色。
第二种输出形式:增加一个非负的阈值,适当选择T,可以使明显的边缘轮廓得到突出,又不会破坏原来平缓的背景。
g(x,y)=⎩⎪⎨⎪⎧gradx,y,grad(x,y)≥Tf(x,y),grad(x,y)≤T第三种输出形式:可以把明显的边缘用一个固定的灰度级LG来表示:
g(x,y)=⎩⎪⎨⎪⎧LG,grad(x,y)≥Tf(x,y),grad(x,y)≤T第四种输出形式:可以把背景用一个固定的灰度级LB来表示,便于研究边缘灰度的变化:
g(x,y)=⎩⎪⎨⎪⎧grad(x,y),grad(x,y)≥TLB,grad(x,y)≤T第五种输出形式:还可以把边缘和背景分别用LG和LB来表示,生成二值图像,便于研究边缘的位置:
g(x,y)=⎩⎪⎨⎪⎧LG,grad(x,y)≥TLB,其他
上述所有算子都是通过求一阶导数来计算梯度的,用于线的检测,在图像处理中,通常用于边缘检测。
在图像处理过程中,除了检测线,有时候也需要检测特殊点,这就需要用二阶导数进行检测。
# 2. 二阶微分法--拉普拉斯
二阶微分在亮的一边是正的,在暗的一边是负的。常数部分为零。
二阶微分定义为:
将一维函数扩展到二维:
二阶微分的定义保证了以下几点:
- 在恒定灰度区域的微分值为0
- 在灰度台阶或斜坡的起点处微分值非零
可以看出,二阶微分可以检测出图像的边缘、增强细节
# Laplacian算子
- Laplace算子作为边缘检测之一,和Sobel算子一样也是工程数学中常用的一种积分变换,属于空间锐化滤波操作。
- 拉普拉斯算子(Laplace Operator)是n维欧几里德空间中的一个二阶微分算子,定义为梯度(▽f)的散度(▽·f)。
- 拉普拉斯算子也可以推广为定义在黎曼流形上的椭圆型算子,称为拉普拉斯-贝尔特拉米算子。
Laplacian算子是线性二阶微分算子,即
∇2f(x,y)=∂2x∂2f(x,y)+∂2y∂2f(x,y)对于离散的数字图像,二阶偏导数可以用二阶差分近似,可以得出Laplacian算子的表达式为:
∇2f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)对应的矩阵算子(卷积核)为
⎣⎢⎡0101−41010⎦⎥⎤(拉普拉斯算子)
# Laplacian增强算子
- 表达式:
- 矩阵算子(卷积核)为
- 算子特点
- 在灰度均匀的区域或者坡度中间二阶差分为0,增强图像上像元灰度不变
- 在斜坡底或低灰度侧形成“下冲”,在斜坡顶或高灰度侧形成“上冲"
- 在图像边缘处理中,二阶微分的边缘定位能力更强,锐化效果更好,因此在进行图像边缘处理时,直接采用二阶微分算子而不使用一阶微分。
import cv2
a=cv2.imread('image\\lena256.bmp')
b=cv2.Laplacian(a,cv2.CV_64F)
b=cv2.convertScaleAbs(b)
cv2.imshow('a',a)
cv2.imshow('Laplacian',b)
cv2.waitKey()
cv2.destroyAllWindows()
2
3
4
5
6
7
8
# 扩展的Laplacian算子
对角线方向上也可以类似组成,
由于拉普拉斯算子是一种微分算子,因此强调的是图像中灰度的突变,并不强调灰度缓慢变化的区域。
拉普拉斯算子是对梯度求散度,在二维图像中,可以想象为二维流场,如果一个点的灰度值比周围低,就是汇聚点 sink,如果一个点的灰度值比周围高,就是发源点source,那么在如果在一个瀑布上,瀑布顶和瀑布低分别是source和sink,也就是可以识别出来。
这将产生把浅灰色边线和突变点叠加到暗色背景中的图像。将原图像和拉普拉斯图像叠加在一起的简单方法,可以复原背景特性并保持拉普拉斯锐化处理的效果。
def laplace2(img, sx = 1.0):
row = numpy.zeros((1, img.shape[1]))
img = numpy.row_stack((row, img, row))
col = numpy.zeros((img.shape[0], 1))
img = numpy.column_stack((col, img, col))
g = numpy.array(((1, 1, 1), (1, -8, 1), (1, 1, 1)))
g = -1 * g
re = numpy.zeros_like(img)
for i in range(1, img.shape[0] - 1):
for j in range(1, img.shape[1] - 1):
re[i, j] = (img[i-1 : i+2, j-1 : j+2] * g).sum()
re = re[1:-1, 1:-1]
return re
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| 原图 | 拉普拉斯滤波 | 增强后的图片 |
|---|---|---|
 |  |  |
# 3. 高通滤波法--高通滤波算子
使用高通滤波算子和图像卷积来增强边缘,常用的算子有:
H1=⎣⎢⎡0−10−15−10−10⎦⎥⎤orH2=⎣⎢⎡−1−1−1−19−1−1−1−1⎦⎥⎤
# 总结
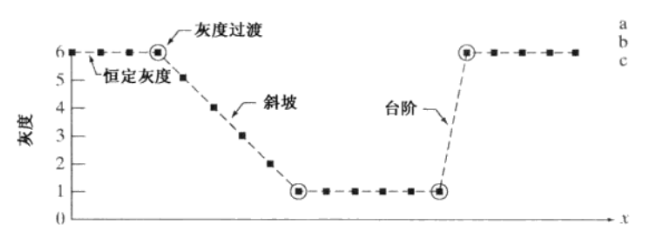
我们使用二阶微分来计算上面坐标中的点的话,就得到下图坐标系中方框所示的点。
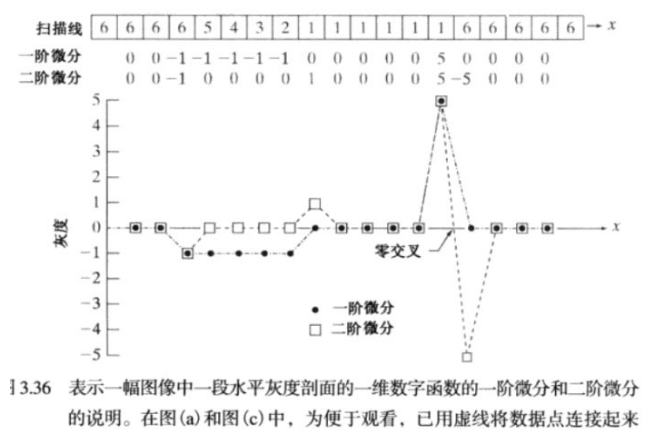
一阶微分——导数大小——高度的变化率——梯度gradient——坡的倾斜程度——边缘只展示一条
二阶微分——导数变化情况——坡的凹凸度——边缘会展示两条
拉普拉斯算子,计算的是当前像素和周围的差异。而索贝尔算子算的其实是 它上面像素 和他底下像素的差异。
梯度是三维的,Laplacian后降维为1,仅保留其强度(散度)
Laplacian的价值就是体现梯度的强度:梯度告诉我们该点的质,而laplacian告诉我们该点的量。
# 图书文献
MOOC《数字图像处理》——武汉大学——4. 图像增强