图像分割-Hough变换

• Hough变换
• Hough变换检测直线
• Hough变换检测直线的原理
• Hough变换的具体实现
• Hough变换检测曲线
  • 具体算法步骤
• 图书文献

Hough变换

Hough变换检测直线

• 检测直线，针对图像上的边缘点，找出其共线的点集及其直线方程.

  • 对于直角坐标系中的一条直线$l$,原点到该直线的垂直距离是$\rho$,垂线与$x$轴的夹角为$\theta$,可以用$\rho,\theta$表示该直线

  • 

  • 直线方程为:

    $\begin{aligned} \rho &= x\cos\theta +y\sin \theta \\ \rho &= x\frac{x_0}{\rho}+y\frac{y_0}{\rho}\\ \rho^2 &= xx_0+yy_0\\ &=[x,y][x_0,y_0]^T \end{aligned}$

  • $\rho^2=[x,y][x_0,y_0]^T$表示从零点到$l$上任意一点$(x,y)$构成的向量在从零点到垂点构成的向量上的向量投影，显然$(32)$为恒等式,即$(29)$恒成立.

  • 所以$l$这条直线用极坐标表示$(\rho,\theta)$,就是一个点.直角坐标系中的一条直线，对应极坐标系中一个点.

  • 

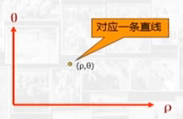
  • 线到点的变换，就是Hough变换.

Hough变换检测直线的原理

• 在直角坐标系中，有任意过一点$(x_0,y_0)$至直线系，这些直线满足:

  $\rho= x_0\cos\theta+y_0\sin\theta=(x_0^2+y_0^2)^{\frac{1}{2}}\sin(\theta+\phi)$

  其中:

  $\phi = \arctan\left(\frac{y_0}{x_0}\right)\\$

• 

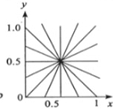
直角坐标系→极坐标系	极坐标系→直角坐标系
这些直线在极坐标系中对应的点$(\rho,\theta)$构成一条正弦曲线	反之，正弦曲线上的一点对应直角坐标系中过$(x_0,y_0)$的一条直线

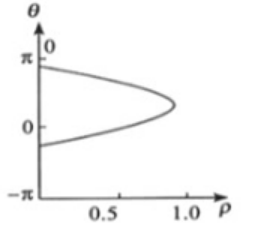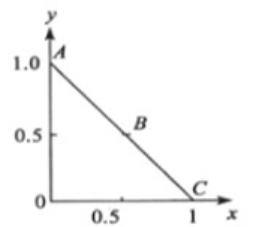如果图像中有若干个点，过每个点的直线系分别对应于极坐标下的一条曲线

• 如果这些正弦曲线有一个共同的交点$(\rho',\theta')$,则这些点共线
• 
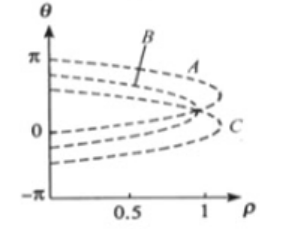
• 且该直线方程为:

$\rho'=x\cos\theta'+y\sin\theta'$

• 相当于该直线$l$上的每一个点的过点直线系放在极坐标成为正弦曲线，这些正弦曲线因为在直角坐标系都有共有的一条直线$l$，因此这些正弦曲线在极坐标系中有一个共交必过点。

Hough变换的具体实现

• Hough变换的实现步骤如下:

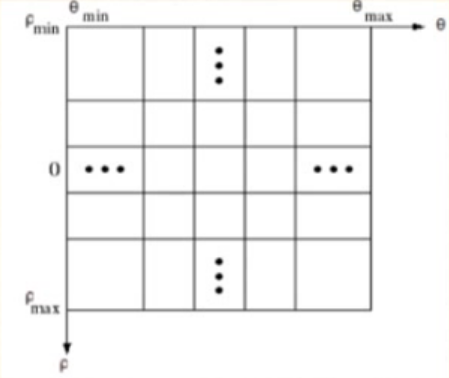
  1. 在$\rho,\theta$极值范围内对其分别进行$m,n$等分，并设一个二维数组$A(m,n)$,用来统计交点计数值.
     • 
  2. 对图像上的所有边缘点做Hough变换，求每个点在$\theta_j(j=0,1,...,n-1)$Hough变换后的$\rho_i$，判断$(\rho_i,\theta_j)$与哪个元素对应，则改数组元素值加1.
  3. 比较数组元素值的大小，最大值所对应的$(\rho_i,\theta_j)$，就是这些共线点对应的直线方向的参数.

• 算法特点：

  • 对$\rho,\theta$量化过粗，直线参数就不精确，过细则计算量增加，因此，对$\rho,\theta$的量化要兼顾参数量化精度和计算量.
  • Hough变换检测直线的抗噪性能强，能够将断开的边缘连接起来.

Hough变换检测曲线

Hough变换的扩展

• Hough变换不只对直线，也可以用于圆:

  • 圆的方程为$(x-a)^2+(y-b)^2=R^2$

  • 与直线相比，圆的参数有$a,b,R$三个，这时参数空间就增加到三维.

  • 若按照直线处理，运算量较大

  • 解决途径:

    • 若已知图的边缘(当然图中还有其他非圆的边沿点混在一起)，而且边缘方向已知，则可以减少一维，把上式对$x$取导数，有
    $2(x-a)+2(y-b)\frac{dy}{dx} = 0$
    • $(36)$式表示参数$a,b$不独立,只需要用两个参数(例如$a$和$R$)组成参数空间，计算量就缩减很多.

• Hough变换不只对直线，也可以用于椭圆:

  • 椭圆的方程为$\Large \frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2} = 1$

  • 取导数有:

  $\frac{x-x_0}{a^2}+\frac{y-y_0}{b^2}\frac{dy}{dx}=0$
  • 已知道椭圆上一点，则只有三个独立参数，只需要从$(a,b,x_0,y_0)$中选取三个参数进行检测.

• 对于任意曲线,

  • 在形状物中可确定一个任意点$(x_c,y_c)$为参考点，从边界上任一点$(x,y)$到参考点$(x_c,y_c)$的长度为$r$,它是$\phi$的函数,其中$\phi$是$(x,y)$边界点上的梯度方向.
  • 
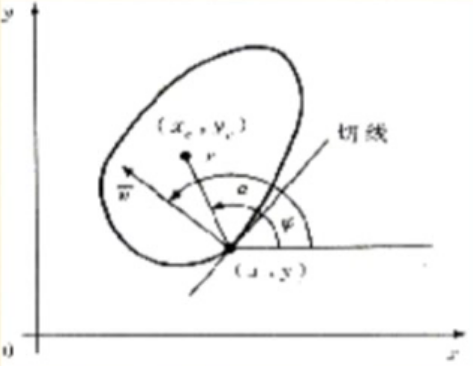
  • 通常把$r$表示为$\phi$的参数方程$r(\phi)$,$(x_c,y_c)$到边界连线的角度为$\alpha(\phi)$,则$(x_c,y_c)$应该满足
  $x_c = x + r(\phi)\cos a \\ y_c = y + r(\phi)\sin a$
  • 对于某已知的边界$R$,可以按$\phi$的大小列成一个二维表格，即$\phi_i \sim (a,r)$表,$\phi_i$确定后可以查出$a$和$r$,经过$(38)$可算得$(x_c,y_c)$
  • 对已知形状建立了$R$表格后，开辟一个二维存储区，对未知图像个点都来查已建立的$R$表，然后计算$(x_c,y_c)$，若未知图像各店计算出的$(x_c,y_c)$很集中，就表示已经找到该形状的边界，集中的程度就是找最大值.

  具体算法步骤

  • 对将要寻找的某物边界建立$R$表，这是一个二维表，以$\phi_i$的步进值求$r$和$\alpha$;

  • 在需要判断被测图像中有无已知某物时，也可对该图某物各点在内存中建立一存储区，存储内容是累加的，把$x_c,y_c$从最小到最大用步进表示，并作为地址，记作$A(xcmin\sim max,ycmin\sim max)$,存储阵列内容初始化为零.

• 对图像边界上每一点$(x_i,y_i)$,计算$\phi(x)$,查原来的$R$计算$(x_c,y_c)$

  $x_c = x + r(\phi)\cos[a(\phi)] \\ y_c = y + r(\phi)\sin[a(\phi)]$

  • 使相应的存储阵列$A(x_c,y_c)$加1.

  • 在这列中找一最大值，就找出了图像中符合要找的某物体边界.

图书文献

MOOC《数字图像处理》——武汉大学——7. 图像分割