图像分割-区域分割

• 区域分割(基于阈值分割)
• 简单图像的区域分割
  • 如何确认阈值$T$
• 复杂图像的区域分割
  • 复杂图像的分割步骤
• 区域增长(区域扩张法)
• 区域分裂合并法
  • 基本原理
  • 具体步骤
• 图书文献

区域分割(基于阈值分割)

简单图像、复杂图像的区域分割

简单图像的区域分割

最简单图像$f(x,y)$	灰度阈值$T$

$g(x,y)= \begin{cases} 1,f(x,y)\le T\\ 0,other \end{cases}$

如何确认阈值$T$

状态法(峰谷法)

• 统计图像的灰度直方图，若直方图为双峰，且有明显的谷；
• 
• 将谷所对应的灰度值作为阈值，再按上面的公示进行二值化.
• 适合于目标与背景的灰度差别较大，且直方图有明显波谷的情况.
• 在应用中，为了便于阈值的选取,可采用灰度加权的方法产生新的直方图,得到更大的峰谷比.

判断分析法

• 假定最简单图像$f(i,j)$的灰度区间为$[0,L-1]$,选取一阈值 $\Large t$ 将图像的像素分为$c1,c2$两组,其中$c1$组像素数为$w1$,$c2$组像素数为$w2$;
• 图像总像素数$w1+w2$,灰度均值为$\Large m=\frac{(m1w1+m2w2)}{w1+w2}$
• 组内方差为:$\sigma_w^2 = w1\sigma_1^2 + w_2\sigma_2^2$
• 组间方差为:$\sigma_B^2 = w1(m1-m)^2 + w2(m2-m)^2=w1w2(m1-m2)^2$

组内方差越小,组内像素越相似,组间方差越大,则两组的差别越大.

• 故$\Large \frac{\sigma_B^2}{\sigma_w^2}$的值越大,表明分割效果越好.
• 改变$t$的取值,使得$\Large \frac{\sigma_B^2}{\sigma_w^2}$最大,这时所对应的$t$,就是分割的阈值.

判断分析法比较便利，是一种常用的方法,但它不能反映图像的集合结构，有时候的分割结果与人的视觉效果不一致。

最小误差分割

• 设图像中背景像素灰度级服从正态分布,概率密度为$p_1(z)$,均值和方差分别为$\mu_1$和$\sigma_1^2$
• 感兴趣目标的像素灰度级服从正态分布,概率密度为$p_2(z)$,均值和方差分别为$\mu_2$和$\sigma_2^2$.
• 
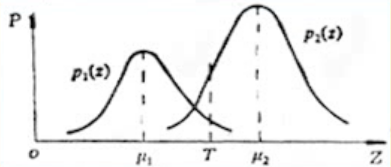
• 设背景像素数占图像总像素数的百分比为$\theta$,目标像素数占$(1-\theta)$,则混合概率密度为:

$\Large p(z)=\theta p_1(z) +(1-\theta)p_2(z) = \frac{\theta}{\sqrt{2\pi}\sigma_1}e^{\frac{-(z-\mu_1)^2}{2\sigma_1^2}} + \frac{1-\theta}{\sqrt{2\pi}\sigma_2}e^{\frac{-(z-\mu_2)^2}{2\sigma_2^2}}$

• 当选定阈值为$t$时,目标像素错分为背景像素的概率为:

$E_2(t) = \int_{-\infty}^{t}p_2(z)dz$

• 把背景像素错分为目标像素的概率为:

$E_1(t)=\int_{t}^{+\infty}p_1(z)dz$

• 则总误差概率为:

$E(t)=\theta E_1(t) + (1-\theta)E_2(t)$

• 为使得$E(t)$最小,可以令$\frac{\partial{E(t)}}{\partial{t}}=0$,即

$-\theta p_1(t) + (1-\theta)p_2(t)=0$

• 当$\sigma_1^2 = \sigma_2^2 = \sigma^2$时,有$t=\frac{\mu_1+\mu_2}{2}+\frac{\sigma^2}{\mu_2 - \mu_1}\ln\frac{\theta}{1-\theta}$
• 若先验概率已知,l例如$\theta=\frac{1}{2}$,则有$t=\frac{\mu_1+\mu_2}{2}$

复杂图像的区域分割

目的:多阈值分割

这幅图中，就有3个类（分别对应0，1，2），因此，我们就需要确定两个阈值 T1 和 T2 。

复杂图像的分割步骤

1. 自动平滑直方图

   一般来说,待分析图像的灰度直方图不是很平滑，这对自动寻找峰与下一步确定阈值带来困难，因此有必要对直方图进行平滑，一般来说，可以采用__空间滤波器__与直方图做卷积来进行平滑.

2. 确定区域类数

   对于灰度层次不多的图像,一个区域类通常对应直方图中的一个峰,但是平滑后的直方图中的每一个峰不一定都对应一个区域类,因而有必要通过检查认定峰对应的区域类.

3. 自动搜索多个阈值

   可以采用前面介绍过的判断分析法,依次计算各峰两两之间的最佳阈值，然后再用这组阈值分割原始图像.

特征空间聚类

• 利用特征空间聚类进行图像分割,可以看成是阈值分割概念的推广.

  • 将图像空间中的像素用对应的特征空间点表示
  • 根据他们在特征空间的聚集情况对特征空间进行图像分割
  • 最后将他们映射会原图像空间, 得到分割的结果.

• K均值聚类算法步骤

  • 任意选择$K$个初始类均值,$\overrightarrow{Z}_1,\overrightarrow{Z}_2,...,\overrightarrow{Z}_K$
  • 使用最小距离判别法将任一样本分给$K$类中的某一类,若对所有的$i\ne j$,有$|\overrightarrow{x}-\overrightarrow{Z}_i| \lt |\overrightarrow{x}-\overrightarrow{Z}_j|$，则$\overrightarrow{x}$属于第$i$类.
  • 根据分类结果，计算各类均值，并以此作为新的类均值.
  • 比较新旧类均值,若他们之差小于某一阈值，则认为中心已经稳定，可以终止算法，输出结果，否则继续使用最小判别法进行分类.

区域增长(区域扩张法)

区域分割(基于阈值)的方法并没有顾及到像素之间的连接性。

区域增长(区域扩张法)顾及到像素之间的连接性。

• 基本原理:

  • 先把图像分割成若干个小区域，
  • 然后比较相邻小区域特征是否相似，若他们足够相似，则作为同一个区域合并，以此将特征相似的小区域不短合并，直到不能合并为止，最后形成特征不同的区域.

• 区域增长根据所用的邻域方式和相似性准则的不同，产生各种不同的区域扩张法.

单一型	质心型	混合型
像素与像素	像素与区域	区域与区域

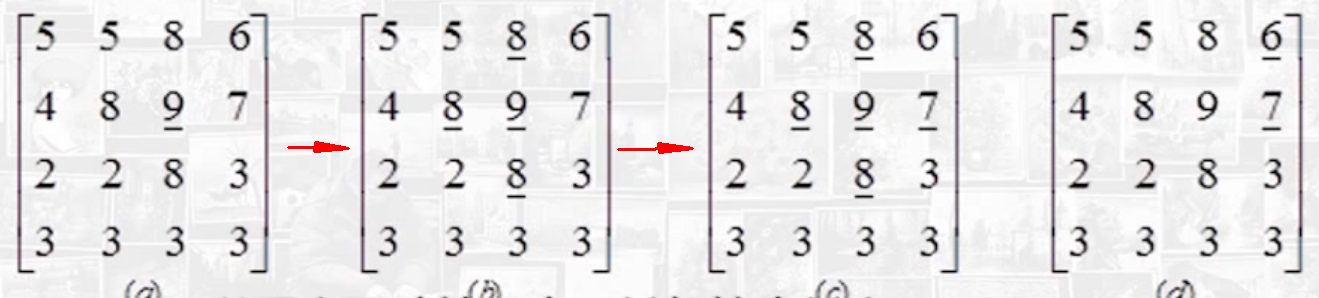
简单区域生长

以像素灰度为特征的简单区域增长法

• 对图像进行光栅扫描，求出不属于任何区域的像素，当寻找不到这样的像素时结束操作.
• 把这个像素灰度同其4-邻域或8-邻域中不属于其他区域的像素进行比较，若灰度差值小于阈值，则合并到同一区域，并对合并的像素赋予标记.
• 从新合并的像素开始，反复进行上一步的操作.
• 反复进行上两步的操作，直到不能再合并
• 返回到第一步，寻找新区域出发点的像素.
• 若两个区域之间的灰度变化比较平缓，则两个区域容易被合并成一个区域，为了规避这个问题，在第二步中，改为比较已存在区域的平均灰度与该前一天有邻接的像素灰度值.

质心型区域生长

就是简单区域生长的改进

质心型链接操作步骤类似简单区域扩张法，唯一不同的是在上述（2）的操作中，改为比较已存在区域的像素灰度平均值与该区域邻接的像素灰度值。若差值小于阈值，则合并。

• 缺点：区域增长的结果与起始像素有关，起始位置不同，在分割结果有差异.

混合型区域增长

把图像分割成小区域，比较相邻的小区域的相似性，相似则合并，知道不能合并位置.

• 不依赖于起始点的方法

  1. 设灰度差的阈值为0，用简单区域扩张法把具有相同灰度的像素合并到同一区域，得到图像的初始分割图像.
  2. 从分割图像的一个小区域开始，求出相邻区域间的灰度差，将差值最小的区域合并.
  3. 反复进行第二步，把区域依次合并，适当阶段停止合并，得到分割图像.

• 假设检验法(根据图像子块内的灰度分布的相似性进行子块合并，最终实现图像的分割)

  1. 把图像分割成不交迭、大小为$n\times n$的子块.
  2. 比较相邻子块的灰度直方图相似性，相似则合并为同一区域
  3. 反复第二步，直到区域不能合并为止.
     • 相似性的判断标准:
       • KS检测标准
       • SD检测标准
  • 难点:子块大小$n$的判断，根据经验$n$一般取$5\sim 10$

区域分裂合并法

使用场景:事先不清楚区域形状和区域数目.

分裂合并法对分割复杂的场景图像比较有效

基本原理

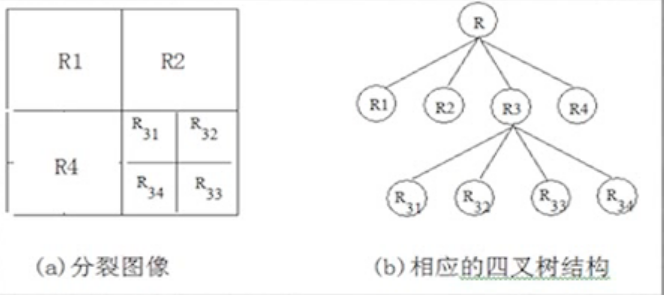
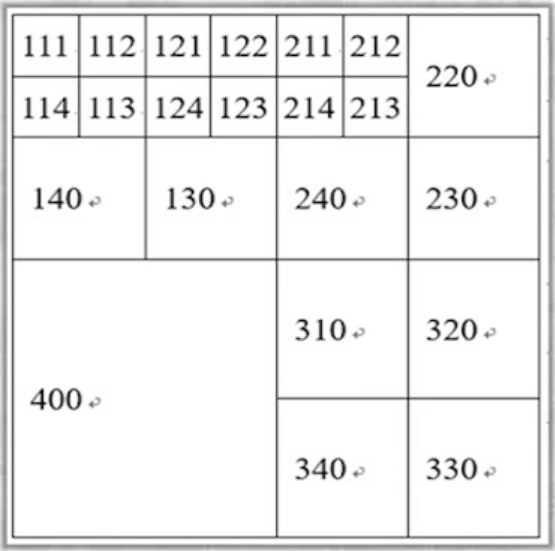
• 基于__四叉树思想__，把原始图像整体作为树根或零层，将图像等分成4块，作为被分裂的第一层.
• 对于第一层的每一个子块，如果个像素属性一致，则不再等分.
• 若属性不一致，则子块须继续分裂成相等的4块，作为第2层，如此循环.
• 块的编号确定方式:
  • 第一层4块，从左上块开始，按照__顺时针方向__编号$1,2,3,4$，第2层以后每一块的标号方式一样，但下一层子块的编号是在它的上一层的标号后添加，当不再往下划分时，其尾数添加0.
  • 

分裂、合并操作原则

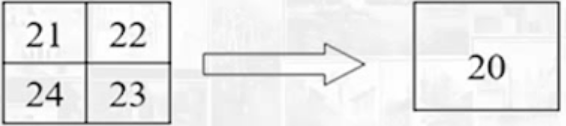
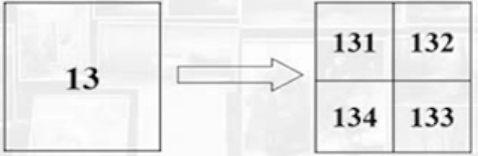
合并	分裂
当同一层的4块像素满足某一特性的均匀性时，就把他们合并为一个母块	当某一层的某一子块内像素不满足均匀条件时，将他们分裂成4个子块

• 均匀性可以看做灰度的均匀性或某种纹理特征的均匀性.

具体步骤

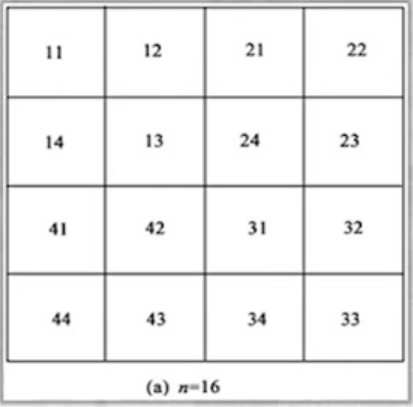
1初始分割	2合并处理	3分裂处理
把一幅图像分裂到第二层($4*4=16$)	按预先给定的合并原则，对第二层的每4个子块进行检查	当第二层的每一个子块内像素不满足特性均匀性条件时，则把他们分裂成4个子块

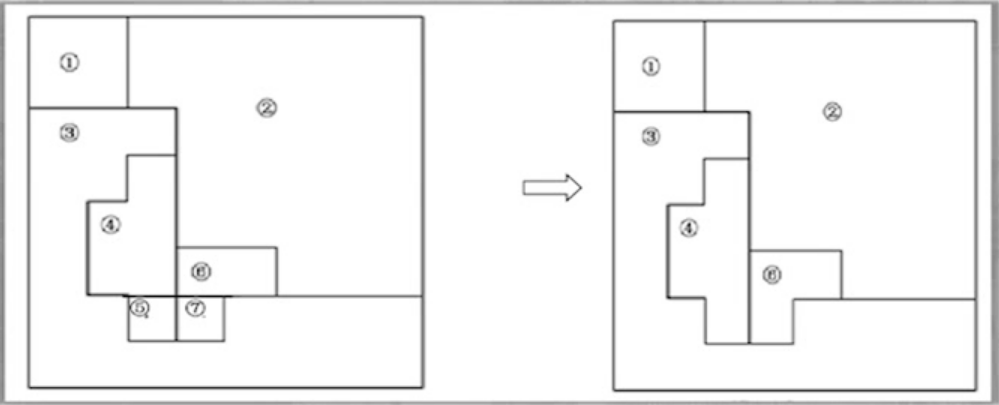
4组合处理	5消失小区
以每块为中心，检查与其相邻的各块，凡符合特征均匀性的，再次合并	将小区与邻近大块进行比较，按他们对邻近大块的均匀性程度分别划到对应区号

图书文献

MOOC《数字图像处理》——武汉大学——7. 图像分割