拉普拉斯变换与Z变换

拉普拉斯变换

导读

傅里叶变换虽然好用，而且物理意义明确，但有一个最大的问题是其存在的条件比较苛刻，比如时域内绝对可积的信号才可能存在傅里叶变换。

拉普拉斯变换可以说是推广了这以概念。即拉普拉斯变换是对傅立叶变换的推广

傅里叶变换是iphone6，则拉普拉斯变换是iphone6s

两个变换本质都是把一个连续函数拆开

• 傅里叶变换，把函数用无限多个正弦波来表示
• 拉普拉斯变换，有些函数无法用正弦波表示，把这类函数衰减一下，再用无限多个正弦波来累加表示

拉普拉斯变换的应用

拉普拉斯变换，是工程数学中常用的一种积分变换。它是为简化计算而建立的实变量函数和复变量函数间的一种函数变换。

• 对一个实变量函数作拉普拉斯变换，并在复数域中作各种运算，再将运算结果作拉普拉斯反变换来求得实数域中的相应结果，往往比直接在实数域中求出同样的结果在计算上容易得多。
• 拉普拉斯变换的这种运算步骤对于求解线性微分方程尤为有效，它可把微分方程化为容易求解的代数方程来处理，从而使计算简化。在经典控制理论中，对控制系统的分析和综合，都是建立在拉普拉斯变换的基础上的。

引入拉普拉斯变换的一个主要优点，是可采用传递函数代替微分方程来描述系统的特性。这就为采用直观和简便的图解方法来确定控制系统的整个特性（见信号流程图、动态结构图）、分析控制系统的运动过程（见奈奎斯特稳定判据、根轨迹法），以及综合控制系统的校正装置（见控制系统校正方法）提供了可能性。

拉普拉斯变换在工程学上的应用：应用拉普拉斯变换解常变量齐次微分方程，可以将微分方程化为代数方程，使问题得以解决。在工程学上，拉普拉斯变换的重大意义在于：将一个信号从时域上，转换为复频域（s域）上来表示；在线性系统，控制自动化上都有广泛的应用。

拉普拉斯变换的数学意义

在自然界，指数信号 $\Large e^{-x}$ 是衰减最快的信号之一，对信号乘上指数信号之后，很容易满足绝对可积的条件。因此将原始信号乘上指数信号之后一般都能满足傅里叶变换的条件，这种变换就是拉普拉斯变换。这种变换能将微分方程转化为代数方程，在18世纪计算机还远未发明的时候，意义非常重大。

$\LARGE F(s)=\int_{-\infty}^{\infty} f(t) e^{-s t} \mathrm{~d} \mathrm{t}=\int_{-\infty}^{\infty} f(t) e^{-(\sigma+i w) t} \mathrm{dt}$

这搞毛呢,不就是傅里叶变换的公式乘以一个 $\Large e^{-\sigma}$ 么,只要搞懂为什么要这么干,我们就能理解拉普拉斯变换了。

我们来看看下面这个信号图：

原信号	$\Large \text{原信号} \cdot e^{-\sigma}$

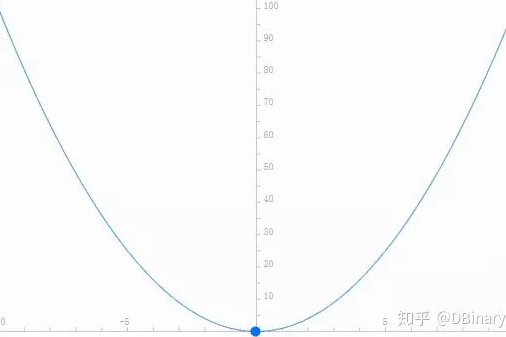这个信号的毛病在于,他已经上天了,是的,它增长的速度太快了,而我们却要使用不能够"上天"的正弦函数去拟合它,这不是为难我胖虎么,这个时候,我们就得想起一句名言,要么解决问题,要么解决制造问题的人(信号),既然傅里叶变换无法制造一个同样上天的正弦信号来拟合,我们就把它原本的信号"掰弯",那么如何"掰弯"呢,简单,乘以一个 $\Large e^{-\sigma}$ 就行了。

拉普拉斯变换的意义无非就是把那些想要上天的函数掰弯,好最终变成那种适合做变换的函数,但是掰弯听起来不太专业,所以我们又管 $\Large e^{-\sigma}$ 叫衰减因子。

拉普拉斯变换是为了解决一些"太飘了"或者专业说法叫不收敛的信号

拉普拉斯变换的物理意义

https://www.bilibili.com/video/av80056198/

• 傅里叶变换通常关注的是不随时间衰减的信号，或者系统在特定频率下的响应。

  • 

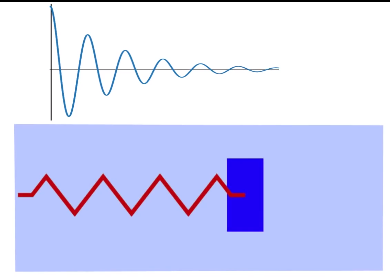
• 阻尼的系统中的响应

  • 

• 而拉普拉斯信号更多关注实际有阻尼的系统中，系统响应的长期变化。两者有紧密的联系。

  • 

傅里叶变换只是拉普拉斯变换中的一部分

时域，频域（傅里叶形式）与复频域（拉普拉斯形式）表达式是对同一组信号的不同表述。

再往大说一点，傅里叶变换，拉普拉斯变换，甚至包括不知道有没有机会讲的小波变换，都在做一件事，将信号在已知的基空间做投影，唯一的区别是基的选取不同。

傅里叶变换	拉普拉斯变换
$\LARGE F(j \omega)= \int_{-\infty}^{\infty} f(t) \mathrm{e}^{-j \omega t} \mathrm{~d} t$	$\LARGE F(s)=\int_{-\infty}^{\infty} f(t) e^{-s t} \mathrm{~d} \mathrm{t}$
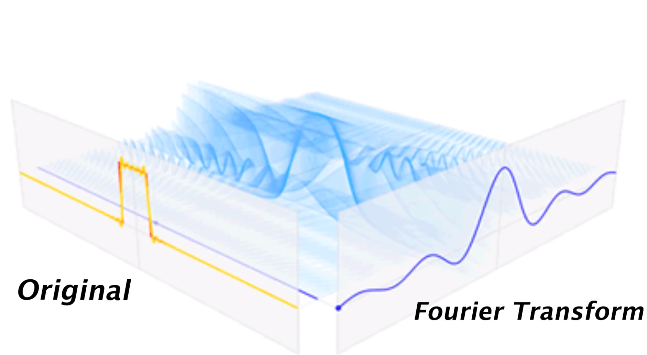	$\sigma \text{和} i\omega$构成 s 平面，含有所有输入s，沿着 $\sigma$ 当衰减因子$\sigma = 0$ 为傅里叶变换结果，切片

https://www.bilibili.com/video/av80056198/

Z变换

导读

在数字信号处理中，Z变换是一种非常重要的分析工具。但在通常的应用中，我们往往只需要分析信号或系统的频率响应，也即是说通常只需要进行傅里叶变换即可。那么，为什么还要引进Z变换呢？

要说到Z变换，可能还要先追溯到拉普拉斯变换。拉普拉斯变换是以法国数学家拉普拉斯命名的一种变换方法，主要是针对连续信号的分析。拉普拉斯和傅里叶都是同时代的人，他们所处的时代在法国是处于拿破仑时代，国力鼎盛。在科学上也取代英国成为当时世界的中心，在当时众多的科学大师中，拉普拉斯、拉格朗日、傅里叶就是他们中间最为璀璨的三颗星。傅里叶关于信号可以分解为正弦信号叠加的论文，其评审人即包括拉普拉斯和拉格朗日。

回到正题，傅立叶变换是最基本得变换，由傅里叶级数推导出。傅立叶级数只适用于周期信号，把非周期信号看成周期T趋于无穷的周期信号，就推导出傅里叶变换，能很好的处理非周期信号的频谱。傅里叶变换虽然好用，而且物理意义明确，但有一个最大的问题是其存在的条件比较苛刻，必须原信号必须绝对可积，比如时域内绝对可积的信号才可能存在傅里叶变换。拉普拉斯变换可以说是推广了这以概念。

在自然界，指数信号 $\Large e^{(-x)}$ 是衰减最快的信号之一，对信号乘上指数信号之后，很容易满足绝对可积的条件。因此将原始信号乘上指数信号之后一般都能满足傅里叶变换的条件，这种变换就是拉普拉斯变换。这种变换能将微分方程转化为代数方程，在18世纪计算机还远未发明的时候，意义非常重大。傅立叶变换不适用于指数级增长的函数，而拉氏变换相当于是带有一个指数收敛因子的傅立叶变换，把频域推广到复频域，能分析的信号更广。

从上面的分析可以看出，傅里叶变换可以看做是拉普拉斯的一种特殊形式，即所乘的指数信号为 $\Large e^{(0)}$ 。也即是说拉普拉斯变换是傅里叶变换的推广，是一种更普遍的表达形式。在进行信号与系统的分析过程中，可以先得到拉普拉斯变换这种更普遍的结果，然后再得到傅里叶变换这种特殊的结果。这种由普遍到特殊的解决办法，已经证明在连续信号与系统的分析中能够带来很大的方便。

然而缺点是从拉普拉斯变换的式子中，只能看到变量s，没有频率f的概念。如果说拉普拉斯变换专门分析模拟信号，那Z变换就是专门分析数字信号，Z变换可以把离散卷积变成多项式乘法，对离散数字系统能发挥很好的作用。

Z变换可以说是针对离散信号和系统的拉普拉斯变换，由此我们就很容易理解Z变换的重要性，也很容易理解Z变换和傅里叶变换之间的关系。Z变换中的Z平面与拉普拉斯中的S平面存在映射的关系，z=exp(Ts)。在Z变换中，单位圆上的结果即对应离散时间傅里叶变换的结果。