场论-基础

# 场的概念

场：如果在全部空间或部分空间里的每一点，都对应着某个物理量的一个确定的值，即在这个空间里确定了该物理量的一个场。（标量场/矢量场、稳定场/不稳定场）

场具备两个宏观属性：能量属性和力属性；这是场的必要性质，如果没有这两个属性就不能称之为场！

实际上，能量和力在微观层面上是等价的，通过量纲分析可知，能量密度的单位J/m³ 和应力单位N/m² 用国际基本单位描述都是kg/(m*s²)。故不可能出现一个场只有能量属性没有力属性，或只有力属性没有能量属性的情况；这与分析力学汉密尔顿原理，储能系统必然对外展示广义力的作用，这一结论完全吻合！

根据物理量的性质，分为标量场和矢量场

标量场（数量场）：物理量是数量。比如：温度场，电位场，密度场等。

矢量场：物理量是矢量。比如：力场，速度场，电磁场等。

稳定场：物理量在各点处的对应值不随时间发生变化（稳态场，静态场）

不稳定场：物理量在各点处的对应值随时间发生变化（瞬态场，时变场）

# 标量场（数量场）

数量场的等值面：数量场u=u(M)（即u=u(x,y,z)），由场中使函数u取相同数值的点所组成的曲面（假设这个函数单值连续且具有连续一阶偏导数，由隐函数存在定理，各连续偏导数不全为零时，这种等值面一定存在）同理可定义等值线。

定义域为 $\large \mathbb{R}^n$ 的多元实值函数

$\mathbb{R}^n \to \mathbb{R}$

$x \mapsto f(x)$

它具有清晰的几何直观。

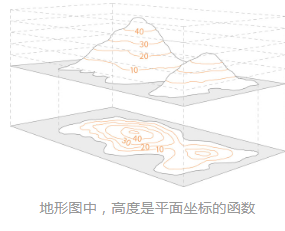
我们也将多元实值函数称为标量场(scalar field)。

# 矢量场

矢量场的矢量线	矢量场矢量面
每一点都与对应于该点的矢量相切的曲线（在流体力学中，此为流线定义）矢量线需满足的微分方程	对于场中任意一条曲线C（非矢量线），在其上每一点处，有且仅有一条矢量线经过，这些矢量线构成矢量面，特别地，当曲线C为封闭曲线时，通过C的矢量面构成管型曲面（矢量管）

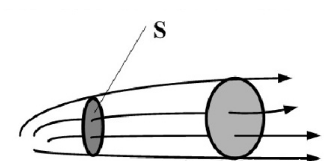定义域为 $\large \mathbb{R}^n$ 的多元实 $n$ 维向量函数

$\mathbb{R}^n \to \mathbb{R}^n$

$x \mapsto f(x)$

也是常见的，如电场、磁场、力场等

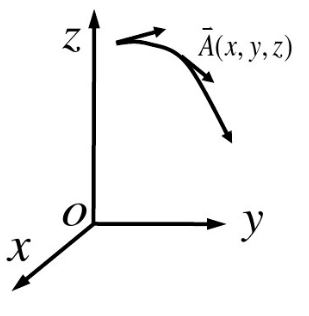
将多元实 $n$ 维向量函数称为向量场(vector field)。

# 标量、矢量和张量

1. 标量

标量是在空间和时间的一个特定点上的，只有大小，没有方向的一个物理量。例如流体的密度，温度和压力都是标量。

2. 矢量

矢量是由两个信息组合而成的物理量，这两个信息包括大小和方向。例如流体单元的空间位置，体积力和速度等都是矢量。矢量包括三个数值，例如速度的表达式如下。

$\vec{u} = \left( u_x, u_y ,u_z \right)$

这里速度的大小为 $|\vec{u}|$ 。

3. 张量

对于应力和应变，我们就需要9个数值组合的张量。这9个值反映了物理量的大小，方向和作用在哪个平面上。

$\bar{\sigma}=\begin{bmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{bmatrix}$

张量其实可以理解为三个平面上的矢量的集合。张量下角标第一个变量代表是在哪个平面，第二个下角标是在哪个方向上的分量。

实际上标量可以认为是0阶张量，矢量是1阶张量，这里的张量本身就是2阶的。

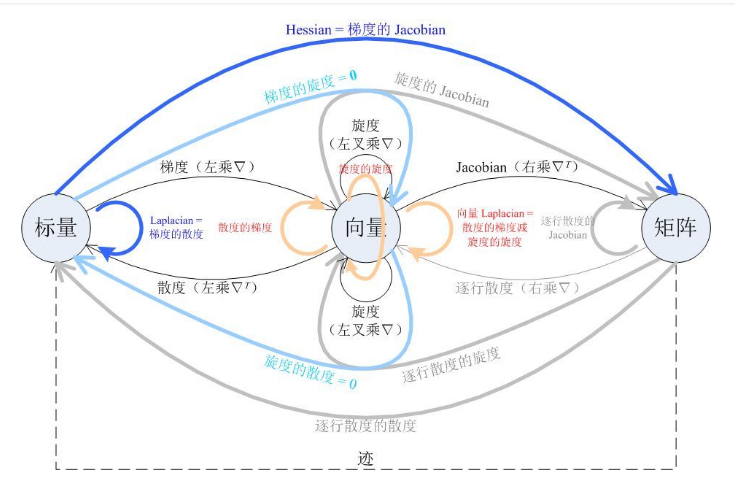
# 梯度、散度与旋度

矢量分析在场论中非常重要，而三个基本算子（梯度、散度与旋度）又是构成各种复杂关系式的基础

# 1. 方向导数与梯度（数量场）

# 方向导数

如果我们从当前点 $x$ 沿着不同的方向步行、骑车或开车，所需要的功率输出是不同的，因为不同的方向，高度 $f(x)$ 的变化率不同。研究这种变化率是非常有实际意义的，如果在规划公路的时候，这种变化率高于车辆可以承受的功率范围，那么车就无法上坡了。一般来说，改变山区高度 $f(x)$ 的成本比较高，所以在设计公路的时候，需要逐点设计公路的方向 $v(x)$ ，使得变化率在车辆功率允许的范围内。

\Large \begin{aligned} \frac{df}{ds} =& \frac{\partial f}{\partial x} \cdot \frac{dx}{ds} + \frac{\partial f}{\partial y} \cdot \frac{dy}{ds} + \frac{\partial f}{\partial z} \cdot \frac{dz}{ds}\\ \frac{df}{ds} =& <\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}> \cdot <\frac{dx}{ds}, \frac{dy}{ds}, \frac{dz}{ds}>\\ =& \nabla f \cdot \vec{v} \end{aligned}

# 偏导数

现在我们需要用到坐标系，在 $\large \mathbb{R}^n$ 中表示点的坐标一般用

$x = (x1, x2, x3, \dots)$

表示，它本质上是自然基的自然坐标表示。

三维矢量可以表达为： $xi+yj+zk$

这里 ${i,j,k}$ 是自然基， ${x,y,z}$ 是坐标表示。

这种直路陡坡，可以理解为公路一直沿着纵横坐标的方向建造。这种情况，方向导数是沿着坐标轴方向计算的。**偏导数(partial derivative)**就是 $f$ 沿自然基向量 $x_i$ 方向（也就是坐标 $x_i$ 方向）求得的方向导数，记为

$\Large \partial_i f = \frac{\partial f}{\partial x_i}$

# 梯度

运算对象是标量，计算结果是向量

# 哈密尔顿算子（Hamilton算子）： $\Large \nabla$

在介绍梯度等概念之前，首先引入CFD非常常见的运算符之一： $\Large \nabla$ ，它是某一物理量在三个坐标方向的偏导数的矢量和，定义如下：

$\Large \nabla = \frac{\partial}{\partial x}i + \frac{\partial}{\partial y}j + \frac{\partial}{\partial z}k$

它具体的含义由下面的式子给出：设 $f$ 是一个可微函数，则

$\Large \nabla \cdot f= \frac{\partial f}{\partial x}i + \frac{\partial f}{\partial y}j + \frac{\partial f}{\partial z}k = grad\ f$

# 哈密顿算子的应用特性

# 梯度（Gradient）

当 $\Large \nabla$ 作用于标量 $f$ 时即可得到该标量在空间中的梯度

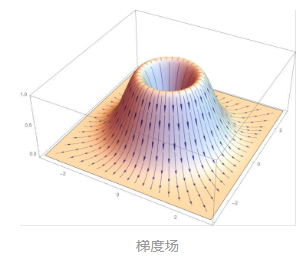
梯度：若在数量场f(M)中的一点处，存在这样一个矢量，其方向为函数f(M)在M点处变化率最大的方向，其模也正好是这个最大变化率的数值，则称G为函数f(M)在点M处的梯度，记作 $grad f$ 。（梯度的定义与坐标系无关，仅有分布决定）

梯度向量是方向导数最大的地方，也就是曲面上最陡峭的方向

梯度在数值计算中有着非常广泛的应用，如共轭梯度法，梯度下降法与梯度上升法等

梯度物理意义为：在某个场中，某点的某物理参数增加最快的方向，梯度大小就是增加率。

举个例子，沿着哪个方向上山，高度上升的速度最快？

这是由高度函数 $f$ 决定的。除非在山顶、山脚、鞍点这类所谓的奇点，在任何一点上都由高度函数在点附近的分布，决定了这样一个高度上升速度最快的方向。整体上，构成一个向量场。

# 梯度的数学表示

把函数在点上沿各个坐标 ${x_i}$ 方向的偏导数（标量）合成一个 $n$ 维向量，称为梯度(gradient)：

$\Large grad f = \nabla \cdot f = \nabla f = [\partial_1f \dots \partial_nf]$

可以看出标量场的梯度是一个矢量场，其分量是各个坐标上的偏导数。它表示 $f$ 在空间某一位置沿某一方向的变化量。

方向导数是方向向量和梯度的双线性映射。将来我们会知道，方向向量和梯度是一对对偶空间

梯度的旋度恒为零向量

「梯度无旋」

# 2. 通量与散度（矢量场）

# 散度(Divergence)

运算对象是向量，计算结果是标量

散度与通量相关，其在电磁学中有着非常广泛的应用

某点散度代表了该点向外的通量体密度，其物理意义可以理解为：定量给出向量场中任一点是否为源点或汇点。

若某点散度等于0，则说明其通量为0，流进=流出；
若某点散度大于0，说明流出>流进，相当于一个源点(source)；
若某点散度小于0，说明流出<流进，相当于一个汇点(sink)。

应用：流体力学中不可压缩条件为：速度场的散度为0。注意此处的推导过程为，不可压缩意味着密度为常数，根据欧拉描述下（基于场的描述）质量连续性方程：

$\frac{d \rho}{d t}+\rho \vec\nabla \cdot \vec v=0$ ,

由于密度为常数，因此其对时间的全导数应为0，因此得出速度的散度为0。

散度表征的是向量场的 发散程度

散度 > 0，表明向量场向外发散
散度 = 0，表明向量场内外平衡
散度 < 0，表明向量场向内聚集

根据矢量点乘的运算规则， $\Large \nabla$ 与一个矢量的点乘是一个标量，它代表了矢量场的散度：

$\Large div\ \textbf{v}=\nabla \cdot \textbf{v}=\frac{\partial u_i}{\partial x_i}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}$

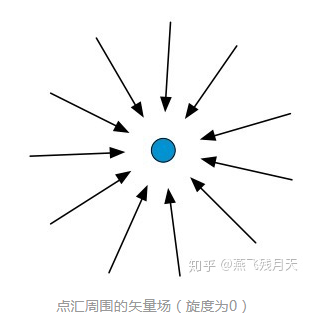
可以看出矢量的散度是一个标量，在CFD中它表示空间中某一区域流入或流出的矢量的多少，比较典型的例子有点源或者点汇。如下图是一个点汇，周围的矢量均流向该点。

# 拉普拉斯算子

拉普拉斯算子包含两部分：梯度外面套了一个散度

通过梯度可以将该element与周围产生的交互表达为作用在该element外界面的量。例如速度的梯度表达了作用在该element外界面上的粘滞应力。又例如温度的梯度表达了作用在该element外界面上的热流。但是这样往往还不够，因为这样所得的量的作用对象是element的外界面。而element的体积是不为零的，它自身所有的量（如速度，温度）是包含在其体积上的，而非外界面上。这时候就需要散度出场了。

根据divergence theorem，散度能将作用在外界面的量转化为作用在element本体的量。这样有了拉普拉斯算子我们就能够很好的把某一element与周围的环境联系起来。不是很恰当的比喻就是梯度搭桥，散度结账。

根据亥姆霍兹定理，无界空间中，只要对力场函数进行一次哈密顿运算，就可以找出源的分布函数，即找到了场源，而由于力场函数是势场函数一阶哈密顿运算结果，所以对力场函数的一阶哈密顿运算就是对势场函数的二阶哈密顿运算，即拉普拉斯算运算！

总结概括地说，拉普拉斯运算从物理上可以理解为通过势函数寻找场源的操作。分析一个场，弄清楚场源的分布极其重要，所以拉普拉斯运算的重要性也就不言而喻了！

标量势函数（如电势函数φ）的拉普拉斯运算结果依然是标量函数（电荷密度与介电媒质的函数，-p/ε），相当于对标量势函数求梯度后再求散度；
旋度场矢量势函数（如矢量磁位A）的拉普拉斯运算依然是矢量函数（电流密度J导磁媒介u的函数**，-uJ**），相当于对矢量势函数求旋度后再来一个旋度操作。

再由以上导数方向与梯度的内容可知

标量的梯度为矢量，因此对该矢量可以继续求散度

从而引入拉普拉斯算子 $\Large \nabla^2$ （ $\Large \Delta$ ）

\Large \begin{aligned} \nabla \cdot \nabla =& ( i \frac{\partial}{\partial x} +j \frac{\partial}{\partial y} + k \frac{\partial}{\partial z} ) \cdot ( i \frac{\partial}{\partial x} +j \frac{\partial}{\partial y} + k \frac{\partial}{\partial z} ) \\[2ex] \nabla^2 =& \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \end{aligned}

拉普拉斯算子是梯度算子和散度算子的叠加运算。该算子一般用于标量场的运算。

$\Large \nabla \cdot (\nabla s)=\nabla^2s=\frac{\partial^2 s}{\partial x^2_i}= \frac{\partial^2 s}{\partial x^2}+\frac{\partial^2 s}{\partial y^2}+\frac{\partial^2 s}{\partial z^2}$

上式代表了梯度的散度，可以看出标量经过拉普拉斯算子运算以后仍然是标量。

矢量的散度为标量，因此对该标量可以继续求梯度：

$\Large \nabla \cdot(\nabla \cdot \vec{\textbf{v}})= \nabla^2 \vec{\textbf{v}}= \nabla^2 u_i= (\nabla^2 u)\textbf{i}+(\nabla^2 v)\textbf{j}+(\nabla^2 w)\textbf{k}$

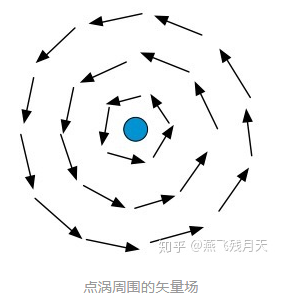
# 3. 环量与旋度（矢量场）

在流动的河面上，水在各处的流速是不同的.因此河面上的一片落叶除了向下游漂去以外，还会自己**「打旋」**.那该怎么刻画旋涡的“强弱呢”？

# 旋度(Curl)

旋度与环量(circulation)联系紧密，其在流体力学中有着广泛的应用，其定义为：

旋度是由 $\Large \nabla$ 与矢量的叉乘得到，它的运算结果是一个矢量，代表了矢量做旋转运动的方向和强度：

\Large \begin{aligned} \nabla \times \textbf{v}=& (\frac{\partial}{\partial x}\textbf{i}+\frac{\partial}{\partial x}\textbf{j}+\frac{\partial}{\partial x}\textbf{k})\times (u\textbf{i}+v\textbf{k}+w\textbf{k})= \begin{bmatrix} \textbf{i} & \textbf{j} &\textbf{k}\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\ u & v & w \end{bmatrix}\\[2ex] =&(\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z})\textbf{i}+(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x})\textbf{j}+(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y})\textbf{k} \end{aligned}

一个典型的有旋流场是点涡，如下图所示，它展示了一个散度为0的有旋矢量场。

君骨书生

Choose mode

场论-基础